计算生物学，应用数学的一个分支

运用数学建模、数据分析等方法解决生物问题

促进数学与生物学的双向发展

数学科学学院小π工作室

特别专访李铁军教授

听他讲述进入计算生物学领域的研究点滴

今天，我们节选部分内容

带你走进“数学+”的魅力世界

一、最初：复杂流体中的间接了解

进入计算生物学这个领域，其实说起来挺偶然的。我博士时的研究跟这个领域一点关系都没有，博士毕业之后，是和张平文老师、鄂维南老师共同合作做复杂流体（complex fluids）。大概做了5～6年的时间。但是复杂流体实际上跟生物是有关系的。所谓复杂流体，就是在普通的流体里面掺杂了很多高分子；其另一个称呼是所谓“流变学”，是研究流体里的高分子影响流体本身运动的学问。

高分子这个东西它自然地跟生物有关系。比如说DNA就是一个非常大的一个高分子。我们知道DNA在细胞体内是高度缠结的，如果把它全部拉长，它能绕地球一周，因此它是一个极大的高分子，蛋白质也都是高分子。所以那个时候做复杂流体就接触高分子；接触高分子时自然就会读到一些和生物有关系的文献，但那个时候的接触是非常间接的，主要还是集中在高分子对流体的影响上。

复杂流体中的polymer

二、tau-leaping方法的数值理论

复杂流体做了段时间之后（大概是5～6年），我意识到我想适当地扩大一下我的研究范围。那时候我从张老师那里博士毕业已经有若干年了，所以我还是希望做一点比较独立的研究。其实任何一个博士毕业之后，都会面临这样一个阶段：你不要老是跟你以前的老板做东西，你需要自己独立地去做一些东西。

受鄂老师和张老师的指引，我把自己定位成要做随机模型和算法的研究。经过一番了解，我发现计算生物学领域里随机算法非常重要，这个领域里一个重要的方法叫随机模拟方法(SSA: Stochastic Simulation Algorithm)。

实际上这种方法现在是计算生物学里面最基本的一个方法，最初由D.T. Gillespie在1970年代提出的。

大概在2002年的时候，他们刚提出一种新的方法，希望把SSA方法进一步推进：他们发现SSA尽管非常好，但是做很多生物模拟的时候速度太慢，因为它在模拟的时候每一个反应都要追踪，如果这个反应非常频繁，它需要消耗非常大的计算量。当时他们希望加速这个方法。

这个新方法叫做tau-leaping方法。D.T. Gillespie是和UCSB的女教授、美国工程院院士Linda Petzold合作做这个。我通常把它翻译成“逃匿法”。因为tau表示时间，leaping就是跨越，所以tau-leaping就是时间跨越，我把它翻译成“逃匿法”，就是说你要逃得快一点。他们提出这个工作是在2002年。

D.T. Gillespie ,已于2017年离世

这个正好是对随机系统的数值模拟的方法，所以很自然引起我的注意。那个时候他们这个领域还发展的不是很多，大概只有几年的时间。当时我就把他们所有相关文献全部都读了一遍，从而形成了自己的一些看法，我开始在“逃匿法”的研究领域里面写了一篇文章。那篇文章应该是2006年写出来的。

这完全是一个数值分析的工作，实际上是证明了他们的“逃匿法”应该怎么样去理解，是不是有收敛性，在数学上应该怎么去做。我们所有做数值分析的人，往往拿到一个重要的数值方法，都会做这样的事情。

Linda Petzold她在工程系，是一个非常有名的计算数学家，她以前主要是做微分代数方程的数值解，在那个领域非常有名气。

但是我觉得他们对随机的这套理论没有那么熟悉。所以我当时读了他们那工作之后，就试图基于随机的这套工具，给他们做的这些方法建立一个基本的收敛性的框架。

那篇文章做了之后，我认为还是受到了很多人的关注。有很多人在跟进我们的那个工作，我觉得还是有相当的影响力的。至少在这个领域，我想几乎所有做“逃匿法”的人大概都知道我们的这个工作。

总而言之，那个时候我接触到的就是在生物里面做计算、做分析，后来我又去试图要做一些更高阶的格式，从计算数学角度来做这样一个问题。

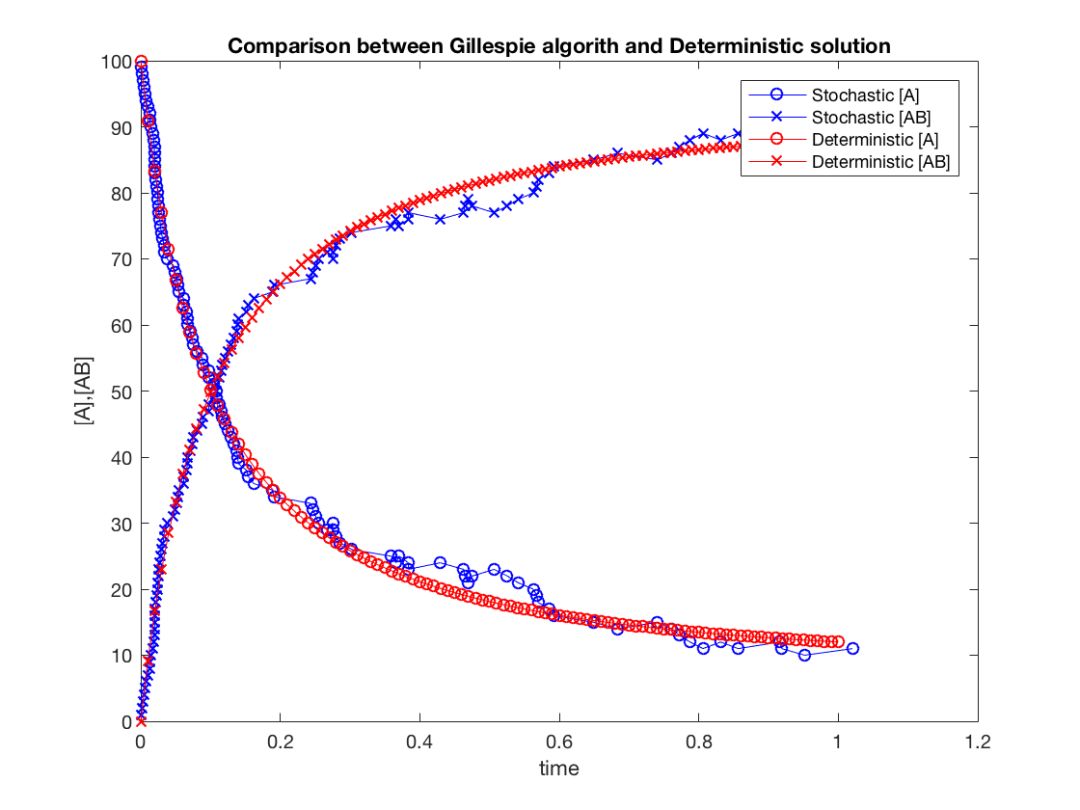
SSA的模拟结果

三、向更实际的情形推进

这个事情又做了几年，我想应该是直到2010年或2011年。我到不同的地方去做报告，就去讲这些东西。我的一个听众是Linda Petzold课题组里的曹阳，他是我在清华念书时的师兄，他是清华数学89级的，我是91级的，他是跟他们合作的“逃匿法”的主要发展者。

我好几次请他到国内来做报告，我也给他介绍我们的工作。他说生物里面数学模型本身误差就很大。为什么呢？生物里有一个现象，你需要建立一个模型去解释。但是生物体系非常不容易进行精确建模。因为你不能杀死这个细胞，你杀死细胞建立的模型那东西没有任何意义。

这和物理不一样，物理的东西都是死的，你可以非常精确的进行控制它，去了解它的运动的规律。但生物体是不行的，是活体，这给整个生物的研究带来一些困难。所以在模型建立过程中，就有很大的误差。

换句话说你现在建立模型，解释现象基本上都是定性的。要是建立了一个模型跟定量的测量值完全对上，这几乎是做不到的。即便你做到了，也不见得有人真正信服你，你就是做fitting，就是为了凑这个数据，而且数据里面噪声也很大，这么做不见得有很大意义。

我这位师兄说，既然模型的误差本身就已经很大了，你去搞一个高阶格式，算那么准，有意义吗？他当时说这个话之后，让我觉得非常frustrated，就是说感到一种挫败感。我们做了这么多数学来做这个事情，难道就是没有意义的？但是不管怎么样，这些事情在我脑子里产生一个印象，就是说做生物你不能完全只是做这些算法的东西，必须要去往更实际的层面和应用的层面去推进。

四、与物理学家的合作

我发现我需要跟生物学家有更多的互动：我要直接进到他们建模或者数据分析的层面。这个时候我想我需要找到一个生物学家，要跟他们合作。所以我也去问当年的师兄曹阳，他说北大物理学院有一位李方廷老师，可以和他聊聊。

我们知道北大生科院这么大，还怕找不到生物学家吗？但是实际的问题是，如果你一个数学家去找生物学家，人家基本上是不理你的。

因为生物学现在停留的阶段还是非常原始的，他们主要做实验、观察现象，数学家去找生物学家聊的时候，他们会觉得：你能够帮助我什么？我观测的是生物学现象，你是个做数学的真的对我有多大帮助？你做推演、做算法，对我实验有帮助吗？

所以一个数学家如果直接去找生物学家，基本上是要碰钉子的。所以我没有去直接去找生物学家，我需要找一个间接的，就是物理学家。

关于数学家、物理学家、生物学家等的一则漫画

物理学家他们能够接触到一些生物的现象，或者说他们跟生物学家有联系，他们在建模，然后数学的人再跟这些模型结合去做方法，这样能有一个过渡，所以我就去找物理学家。物理学里面也有些人做生物的，比如欧阳颀教授，还有汤超教授，以及他们的那些学生。但我首先了解的是我师兄曹阳给我介绍的李方廷老师。他说他也做一些生物学实验，在物理学家中也许可以去找他一下。

其实物理学家对数学家的反应也是类似的，就是你能帮我们做什么？所以我在从数学逐渐走向生物的过程是不顺利的。就是基本上最开始，他们对你没有信任感。但不管怎么样，我说我以前做了些什么样的东西，可以在讨论班上介绍一下我的工作。介绍之后就先建立了一个初步的联络。然后这个时候我们就共同的进行讨论，他的讨论班我就主动去参加。这需要放下身段来，不能总想着我现在是一个数学学院的教授。如果这样合作不可能进行下去，所以我必须要去参加他们的讨论，然后慢慢知道他们在做些什么东西。这个时候他们有一些感兴趣的文章，我们从这里面共同来寻找合作的点。

和我的合作者接触了大概一年多之后，发现做物理的人相对来说对模型这些东西还是很感兴趣的，他们不像生物学家。所以我们找到了一个可以共同合作的点，这个点从数学角度来说，就是生物体系的能量景观。我发现那些物理学家或者是化学家他们非常感兴趣的“能量景观”，包括生物体系中的能量景观，恰好和我以前从鄂老师那学到的所谓“稀有事件”(Rare Event) 非常有关系。

能量景观示意图

然后我们就开始合作，写了好几篇关于这个领域的文章，文章还是有点数学和物理交叉的味道。我们做了一个叫化学反应“两尺度大偏差”的理论，这个本身是一个数学的理论。

当时他们生物的人（应该是生物物理学家而不是严格的生物学家）发现了一个非常有趣的一个生物物理的模型，那个模型里面就存在我们所感兴趣的稀有事件，但是没有一个数学的理论去描述它。

物理学家有一套办法，你如果上我的课或者上一些应用数学的课的话，你会慢慢了解到物理学家有一些非常神奇的办法，那些都不是数学家所采用的办法，他们都是不严格的。比如说这里面有一个非常有名的叫Feynmann路径积分，这是非常不严格的一个做法，类似的还有Dirac提出的所谓delta函数等等。物理的人掌握一套这样的工具去做一些问题的时候，能够很快得到一些认识；但这些认识你要去数学上处理，实际上是不好做的。

所以当时我们就对他那个东西给出了一个数学的框架。以往的数学理论不能够涵盖他的结果。后来经过我们的一些思考，发现其实也可以有一套非常好的数学理论，就是所谓化学反应的“两尺度大偏差”。

我们关于这个领域写了若干篇文章，这是和他们的一个初步的合作。做了之后，我想我们彼此的信任感增强了。这个时候我们的合作者做了一些关于单细胞的实验，关于芽殖酵母细胞周期S期检查点激活机制的实验。这些实验要去做一些数据分析，然后建模，去理解机理。因为他觉得我们是可信任的，我们有共同的研究动机，彼此说的语言也都能理解。所以他就把这些数据交给我们来分析。事实上是我们共同来分析，我这边有一个研究生，他那边有研究生，这个工作持续了很长的时间，这是关于动力学的一个故事。

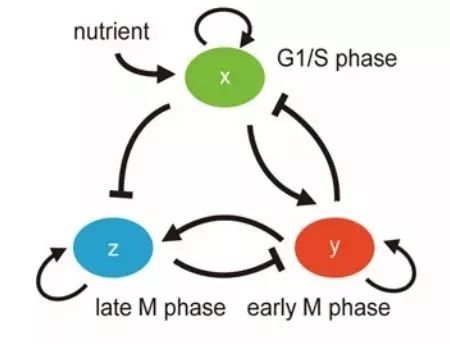
芽殖酵母细胞周期示意图

五、生物信息学的广阔天地

在我从事计算生物学研究的过程中，我渐渐体会到数学在生物里面的应用大概可以分成两类。

一类是动力学的，可能我和张磊都更接近这个些，就是对于生物学的现象，希望通过微分方程，或者随机微分方程，用动力系统的的语言去描述；

但是还有一类非常重要，数学也可以在里面发挥重要作用的叫生物信息学。我们这边比如邓明华、席瑞斌老师。他们是这方面的专家，他们一直是从事这方面的研究，就是说生物里面有大量的数据，比如测序的数据，以及现在大家非常热门的叫单细胞的转录组数据等。

现在这些技术越来越发达，大量的数据产生出来，那问题在于有了这些数据之后，我们怎么样去理解这些数据？怎么样能够给出一些对生物体系的认知？这就是生物信息学所做的事情。

因为这里面没有动力学，非常流行的是通过统计学，通过统计模型的方法去认识这些数据，而且这个领域非常大，甚至在某种意义上可以说这个领域比用动力学方法的领域还要大。

我觉得做计算数学的人，你要在生物里想要得到更大的成就，你就要进到他们内部，去做一点真的有影响力的事情。你希望你的工作能够不仅仅只是在停留在数学的层面，你需要去真的影响做生物的人，我觉得这是一个非常重要的方面。我也把我的一些学生投入进来共同做这样的问题，其中一个集中关注的问题就是现在非常热门的单细胞转录组数据分析。同样最开始进去的时候，也是通过和另外一个老师合作，是中科院上海生科院的陈洛南教授。

我在做这些研究的过程中，慢慢不断认识那些做生物物理的人，做生物信息的人，或者是介乎于生物和数学之间比较交叉的人。然后我在这里面寻找一些可能的我觉得有意义的合作者。第一，不是所有人都会愿意跟你合作；第二也不是所有人你去跟他合作都最好。你需要了解对方，你要两边都能很好地交流，而且对方确实是做的有意思的事情，你必须要确认这一点。

现在我和上海的陈洛南老师保持非常好的研究合作关系。我从他那里了解到一些有意思的、大家正在感兴趣的重要问题，包括一些生物信息学的问题。然后我就和我的一些学生共同来思考这些问题。最近我有一位博士生周沛劼，他今年博士毕业，他在单细胞转录组数据分析这方面做出了非常漂亮的工作。

我们最近和汤富酬教授的研究组共同发展了一个方法，这个方法现在正应用于小肠数据的分析，同时我们也通过他们跟北医三院的一位大夫合作进行小肠癌数据的分析。现在我们有非常密切的交流，每个星期我们的学生都在一起进行组会，讨论一些最新的进展。结合了新的计算方法、实际数据分析以及医学的应用，我觉得这个工作会是一个极其漂亮的成果。

如果我们问这到底是计算数学的还是统计的事情？我觉得其实用不着去严格地去做这个区分。总的来说我觉得我接触生物是一个逐渐进入的过程。原来我是做计算数学的，然后慢慢地做复杂流体，然后跟生物有接触，然后先做动力学，先做数值方法，比较偏理论，然后逐渐的要去做模型，然后就是想要去分析生物学数据，是一个逐步前进的过程。整个的过程其实是一个摸索的过程。

六、生物对数学对刺激

我们把数学应用到生命科学中，试图以数学为工具解决一些生命科学的问题和一些现象，自然是希望能够对他们有帮助。

但我还要强调一点，就是我们毕竟是数学出身，应该同时要反过来想一想，生命科学是不是有可能产生一些东西对数学会有影响。从这里面也许能够提炼出一些好的数学概念或者定理，或者一些方法。这件事情我觉得也是永远要记在脑袋里面，希望能够“反方向”有一个作用，思考他们是不是也对我们的数学能够有一些刺激？

七、生物中的数学：魅力无穷

最后我想说一下，这也是我想要传达的一个重要观念。做生物数学，如果用经典的或者传统的计算数学眼光去看，往往会觉得里面数学的东西不够多，而且似乎也不够难。但其实这是因为生物里面很多问题还没有被理解清楚。很多时候待研究的数学问题是什么其实是需要你和生物学家反复沟通才逐渐提炼出来的。

但是我要强调，这才是生物数学的魅力所在。当然这和个人的性格爱好有关系。杨振宁先生说过一句话，他说进入一个领域，一定要在这个领域还不是很成熟的时候，你进去做，你才有希望能够做出真正大的、有意思的东西。如果这个领域已经被发展得非常完善了，你再进去，对不起，已经没有空间了，房子全都被人家盖好了，你进去就欣赏一下，转一圈，难以有大的贡献了！生物数学不是这样。它是一个没有完工的房子，这个房子很多地方还没盖起来，很多地方是空的，你进去了有很大的发展空间，也可以自己马上动手来添砖加瓦。

我认为对想要从事应用数学的人来说，一定要有这个意识。传统教育教出来的学生往往会有这样一个习惯：喜欢接触到很干净、很确定的东西。但是事实上科学研究中的很多数学问题提法并不很清楚，但科学问题是实打实地放在那里，是清楚的，是极有意义的。你怎么样去从数学的角度，用数学的语言去提炼它，用合适的数学工具去解决它？你怎么样去设计方法？这正是数学生命科学的魅力。

这和个人性格、个人气质也有关系。每个人都要意识到自己的性格特点和长处，这很重要。还有做应用往往需要你比较open。如果你不open，做这些交叉学科，不去跟那些做物理和生物的人交流，不去跟他们做朋友，你就了解不到那些最有意思的问题。因为完全停在数学里面冥想是不够的，交叉学科就是很多事情说不清楚，有些问题你需要通过跟他们聊才能了解到这个问题。他们感兴趣的问题是什么？有意义的问题是什么？

人物简介

李铁军（2020年度北京大学优秀工会积极分子）

北京大学数学科学学院教授，信息与计算科学系副主任。1995年获清华大学学士学位，1998年获清华大学硕士学位，2001年获北京大学博士学位。主要研究方向为随机模型及算法。

来 源：学生工作办公室、小π工作室

访谈作者：黄 桢、谢鹏志

责 编：牛 贺、任 燃

排 版：任 燃